1070. Fill the line
n segments are
colored on the number line. The coordinates of the left and right endpoints of
each segment, li and ri, are
given. Find the total length of the colored part of the number line.
Input. The first line
contains the integer n (1 ≤ n ≤ 15000). The next n
lines contain two integers li and ri
(-109 ≤ li
≤ ri ≤ 109)
– the coordinates of the endpoints of the segments.
Output. Print the total
length of the colored part of the number line.
|
Sample
input |
Sample
output |
|
5 6 8 1 2 0 3 7 9 2 4 |
7 |
SOLUTION
geometry – sweeping line
Algorithm analysis
Store the endpoints of the n segments in an array v, keeping track of whether
each point is a left or right endpoint. Then sort the 2 * n points by their x-coordinate v[i]. Next, move from left to right through the intervals (v[i], v[i + 1]) between the points, simulating a sweep line.
Maintain a variable depth,
which represents the number of segments covering the interval (v[i], v[i + 1]). Initially, depth is set to 0. Increase
depth by 1 when encountering a point that is the start of a segment and
decrease it by 1 when encountering a point that is the end of a segment.
The total length of the
painted portion of the line is the sum of the lengths of intervals xi+1 – xi, where depth ≠ 0.
Example
Let us consider the set of
the following segments:
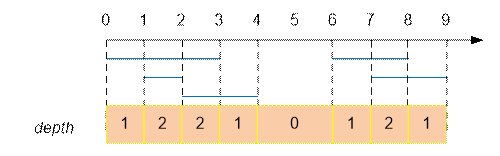
The answer is
the sum of the lengths of the intervals xi+1 – xi, where depth ≠ 0.
Algorithm implementation
The endpoints of the segments will be stored in an array v as
pairs: (x-coordinate of the point, label indicating whether it is the start
or end of a segment).
vector<pair<int, int> > v; // (x, flag),
flag: 0 = Left, 1 = Right
Read the segments and form an array
of points.
scanf("%d", &n);
for (i = 0; i < n; i++)
{
scanf("%d %d", &Left,
&Right);
v.push_back({Left,
0}); // start of a segment
v.push_back({Right,
1}); // end of a segment
}
Sort the points by their x-coordinate.
sort(v.begin(), v.end());
Maintain the depth of overlap (the number of segments covering the current interval) in the
depth variable.
depth = 0;
The length of the painted portion of the line is
computed in the variable res.
res = 0;
Move through
the
points from left to right. For each value of i, consider the
interval [v[i].first, v[i + 1].first].
·
If the point v[i] is
the start of a segment,
increase the depth by 1.
·
If the point v[i] is the end of a segment, decrease the depth by 1.
If depth > 0 on the current
interval, the
interval is considered painted, and its length is added to res.
Since array v contains 2 * n points, the
loop will iterate
over 2 * n – 1 intervals.
for (i = 0; i < v.size() - 1; i++)
{
if (v[i].second == 0) depth++; else depth--;
if (depth > 0) res += v[i + 1].first - v[i].first;
}
Print the answer.
printf("%d\n", res);
Algorithm implementation –
class
Declare a class Point, which stores the x-coordinate
of the point and a label c (which indicates whether the point is the
start or the end of a segment).
class Point
{
public:
int x;
char c; // 'b' – start of segment,
'e' – end of segment
Point(void)
{
x = 0; c = '-';
}
Point(int x, char c) :
x(x), c(c) {};
};
Point p[MAX];
The function f
is a comparator for sorting the points by their x-coordinate.
int f(Point a, Point b)
{
return a.x < b.x;
}
The main part of
the program. Read the segments. Construct an array of points.
scanf("%d",&n);
for(i = 0; i < 2 * n; i += 2)
{
scanf("%d %d",&x,&y);
p[i] = Point(x,'b');
p[i+1] = Point(y,'e');
}
Sort the points by their x-coordinate.
sort(p, p + 2 * n, f);
Simulate the movement of the sweep
line from left to right.
depth = len = 0;
for(i = 0; i < 2*n - 1; i++) // move along the interval [p[i]...p[i+1]
{
if (p[i].c == 'b')
depth++;
if (p[i].c == 'e')
depth--;
if (depth > 0) len += p[i+1].x - p[i].x;
}
Print the answer.
printf("%d\n",len);